Add support for Big Integers (numbers greater than 18446744073709551615) in C along with basic mathematical operations and functions.
Objective
Project Context
Languages like C++/Java support classes like BigIntegers allowing developers to utilize numbers with upto a 100 digits. INTAL aims to provide support upto a 1000 digits in the C language along with basic mathematical operations (comparison, addition, subtraction, multiplication) and some mathematical functions (Fibonacci series, factorial).
Project Stages
The project consists of the following stages:
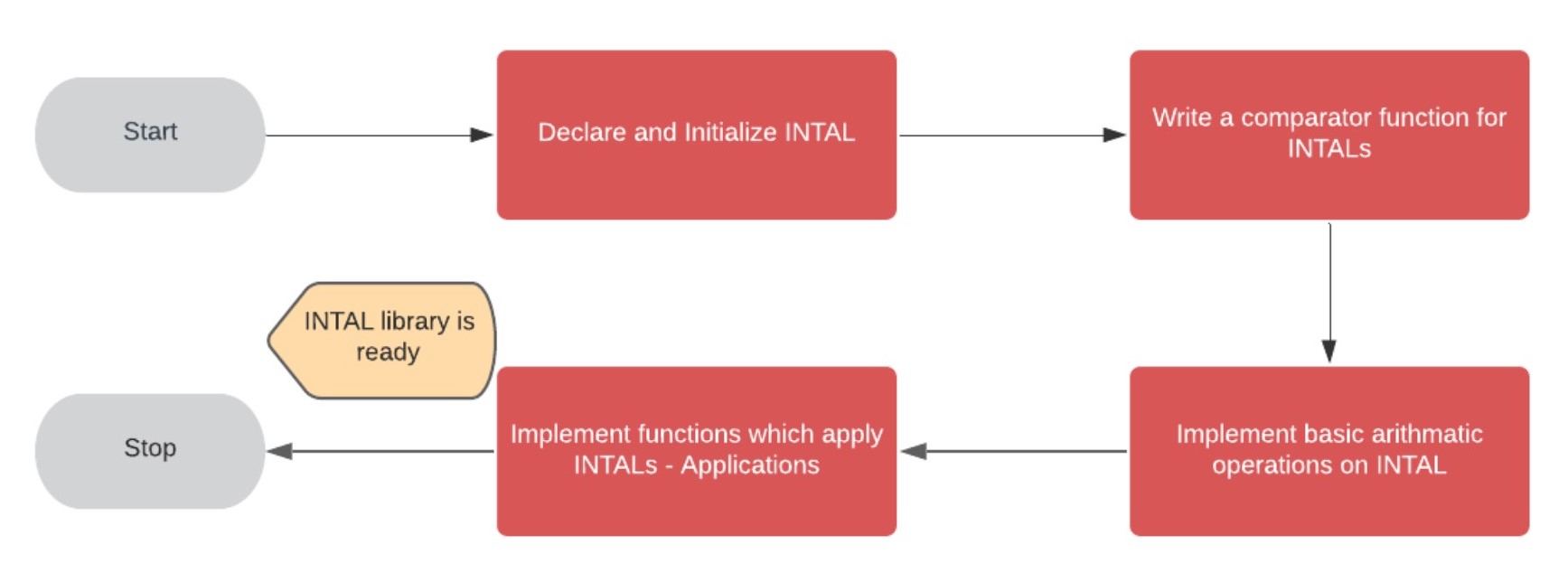
High-Level Approach
- Write a function to declare and initialize INTALs
- Write a function to compare INTALs; returns equal, lesser than or greater than comparisons of inputted numbers.
- Implement basic arithmetic operations on INTAL : Addition, Subtraction, Multiplication
- Implement applications of INTAL: Fibonacci number, Factorial
Applications
- Calculate factorial of very large integers
- Calculate very large nth Fibonacci number
- Calculate binomial coefficient of very large numbers
- Perform binary exponentiation on very large numbers or raise numbers to very large powers
- Greatest Common Divisor
Objective
Add support for Big Integers (numbers greater than 18446744073709551615) in C along with basic mathematical operations and functions.
Project Context
Languages like C++/Java support classes like BigIntegers allowing developers to utilize numbers with upto a 100 digits. INTAL aims to provide support upto a 1000 digits in the C language along with basic mathematical operations (comparison, addition, subtraction, multiplication) and some mathematical functions (Fibonacci series, factorial).
Project Stages
The project consists of the following stages:

High-Level Approach
- Write a function to declare and initialize INTALs
- Write a function to compare INTALs; returns equal, lesser than or greater than comparisons of inputted numbers.
- Implement basic arithmetic operations on INTAL : Addition, Subtraction, Multiplication
- Implement applications of INTAL: Fibonacci number, Factorial
Applications
- Calculate factorial of very large integers
- Calculate very large nth Fibonacci number
- Calculate binomial coefficient of very large numbers
- Perform binary exponentiation on very large numbers or raise numbers to very large powers
- Greatest Common Divisor
Getting Started
Declare character arrays which are the data structure to be used to present INTALs and initialize elements to 0.
Requirements
- You may assume all INTALs are at most 1000 digits long, hence using
mallocfunction, declare a 1001 element character array. The 1 extra element will be for the null character\0. - To avoid computing with garbage values, initialize all elements of the declared INTAL to
0. - The aforementioned guidelines can be treated as a single function which returns 1001 digit INTAL initialized with zeros. This will be useful later on when trying to instantly create an INTAL.
Tip
- Pseudo code
//pseudo code
char* initializeINTAL()
startfunction
//malloc syntax
<datatype>* <pointer-name> = (<datatype>*)malloc(n*sizeof(<datatype>);
// n is number of pointers required
for i = 0 to 1000
do
<pointer-name>[i] = '0'
endfor
<pointer-name>[1000] = '\0'
return <pointer-name>
endfunction
Expected Outcome
You should have declared a function which takes no parameters and whose return type is char*. The function will create an INTAL, initialized to zero and return it to the calling function.
INTAL Comparator
Write a function which compares two INTALs.
Requirements
- Write a function that accepts two INTALs as function parameters and returns
0or-1or1if both INTALs are equal or first INTAL is lesser than second INTAL or second INTAL is lesser than first INTAL respectively. - The function must run in O(n) time (complexity), where n is the number of digits in INTAL or the number of characters in the array.
- INTALs passed to the comparator may be of unequal length and should be kept in mind while determining which INTAL is greater.
References
Tip
- Pseudo code
//pseudo code
int compareINTAL(intal_a, intal_b)
startfunction
//intal_a = {'1','2','3','\0'}, intal_b = {'2','3','\0'}
if length of intal_a > length of intal_b
return 1
//intal_a = {'2','3','\0'}, intal_b = {'1','2','3','\0'}
if length of intal_a < length of intal_b
return -1
i = length of intal_a
//intal_a = {'2','2','3','\0'}, intal_b = {'1','2','3','\0'}
// equal length INTAL
while i > -1:
if intal_a[i] > intal_b[i]:
return 1
if intal_a[i] < intal_b[i]:
return -1
i-=1
// all characters are equal
return 0
endfunction
Expected Outcome
Your function should be able to correctly identify the larger INTAL.
INTAL Adder
Write a function which adds two INTALs and returns their sum.
Requirements
- Write a function that accepts two INTALs as function parameters and returns the sum of both INTALs.
- The function must run in O(n) time, where n is the number of digits in INTAL or the number of characters in the array.
- INTALs passed to the adder may be of unequal length and should be kept in mind while determining sum of INTALs.
- Use the same concept of elementary mathematical addition for adding the INTALs, i.e., basically in case the ith element exceeds
9, a carry over needs to be made to the next element. - Example:
A = {'9','9','9','\0'}
B = {'1','\0'}
Result = {'1','0','0','0','\0'}
- Try visualizing the Additions link provided in references.
References
Tip
- Trouble with logic?
- Compare both the INTALs and find the larger INTAL
- Initialize result INTAL
- Sum of each digit will be
intal_a[i] + intal_b[j] + carry - 96, whereintal_a[i]is the ith digit andintal_b[j]is the jth andcarryis a flag incase there has been a carryover from the previous digit addition. Finally you subtract 96 to get the numerical value. result[k]will be48 + numerical value obtained in previous step mod 10carrywill besum divided by 10- Repeat the process through the entire INTAL.
- In case there is a carry at the end, initialize
result[k]to48+carry
Expected Outcome
Your function should be able to do basic addition on the given INTALs and return the result.
INTAL Subtractor
Write a function which subtracts two INTALs and returns their difference.
Requirements
- Write a function that accepts two INTALs as function parameters and returns the difference.
- The smaller INTAL must always be subtracted from the larger INTAL; so that the result INTAL is always greater than or equal to zero.
- The function must run in O(n) time, where n is the number of digits in INTAL or the number of characters in the array.
- Use the same concept of elementary mathematical subtraction, i.e., basically in case the ith element of the subtrahend exceeds the ith element of the minuend, use the concept of borrow from the neighbouring element of subtrahend. Keep borrowing until found.
- The result INTAL must not contain any preceding zeros in the result, unless the result is zero in which case the INTAL can contain only 1 zero.
- Example:
A = {'1','0','0','0','\0'}
B = {'1','\0'}
Result = {'9','9','9','\0'}
A = {'1','0','0','0','\0'}
B = {'1','0','0','0','\0'}
Result = {'0','\0'}
References
Tip
- Trouble with logic?
- Compare both the INTALs and find the larger INTAL
- Initialize result INTAL to zero
- Start by subtracting elements of the subtrahend by minuend if all elements are less than than of the subtrahend.
- When an element greater than the subtrahend is encountered, look for the element to the right which can donate. Once found subtract one from that element and add 9 to all intermediate elements. Add 10 the element in need of borrowing.
- Repeat above steps until all elements are subtracted.
- Write a separate function to which you pass the result and remove any preceding zeros.
Expected Outcome
Your function should be able to do basic subtraction on the given INTALs and return the result.
INTAL Multiplier
Write a function which multiplies two INTALs and returns their product.
Requirements
- Since our INTALs support a maximum of 1000 digits, the sum of digits of both multipliers must not exceed 1000.
- Write a function that accepts two INTALs as function parameters and returns the product.
- In case either of the INTALs are zero, return zero.
- In case either of the INTALs are 1, return the other INTAL.
- The function must run in O(n2) time, where n is number of digits in INTAL
- We assume intal_b is smaller than intal_a, then perform a check and pass the larger INTAL to a helper function for multiplication as parameter 1 and smaller INTAL as parameter 2.
- Visualize the multiplication of 3 digit numbers to understand the implementation better. Refer to the multiplication video in references.
References
Tip
- Pseudo Code
char* multiplyINTAL(intal_a, intal_b):
startfunction
initialize result
if intal_a is zero or intal_a is one:
copy intal_b to result
return result
if intal_b == 0 or intal_b is one:
copy intal_a to result
return result
l2 = length of intal_b
l1 = length of intal_a
for i = l2-1 to 0:
do
sum = 0, carry = 0, ptr1 = 1
ptr2 = l1+l2-ptr1
for j = l1-1 to 0:
do
sum = (intal_a[j]-'0')*(intal_b[i]-'0') + (result[ptr2]-'0')+carry
result[ptr2] = 48+sum%10
carry = sum/10
--ptr2
endfor
if carry:
res[ptr2] += carry
endif
++ptr1
endfor
return result
endfunction
Expected Outcome
Your function should be able to do basic multiplication on the given INTALs and return the product. By the end of this milestone, you have a basic library of arithmetic functions for INTALs. The coming milestones apply most of the current implemented functions, so make sure you successfully implement these first.
INTAL Fibonacci
Write a function which returns the nth Fibonacci INTAL.
Requirements
- Write a function to take an
unsigned int nas parameter and return the nth Fibonacci INTAL. - Refer to the algorithm to compute the nth Fibonacci number. The only additional logic is required to deal with INTALs.
- Have 2 INTALs initialized to Zero and One respectively.
- Until n terms are generated, keep adding the previous 2 Fibonacci terms as is with the Fibonacci algorithm.
- It is recommended to compute the nth Fibonacci INTAL in constant space because computing all intermediate results and not reusing them may deplete system memory. Refer Method 3 of Fibonacci in references.
References
Tip
- Pseudo Code
char* FibonacciINTAL(unsigned int n):
startfunction
initialize intal_a to zero
if n is zero:
return intal_a
endif
initialize intal_b to one:
if n is one:
free intal_a
return intal_b
endif
initialize intal_temp to zero
for i = 2 to n:
do
temp = addINTAL(intal_a, intal_b)
free intal_a
intal_a = intal_b
intal_b = temp
endfor
free intal_a
return intal_b
endfunction
Expected Outcome
Your function should return the nth Fibonacci INTAL. You should have your first working application of implementing INTALs in C.
INTAL Factorial
Write a function which returns the factorial of that number.
Requirements
- Write a function to take an
unsigned int nas parameter and return the factorial represented as an INTAL. - The concept of factorial of a number remains unchanged. Your part is to incorporate INTAL computations into the algorithm.
- It is recommended to compute the factorial INTAL in constant space because computing all intermediate results and not reusing them may deplete system memory and take longer than expected.
References
Tip
- Pseudo Code
char* factorialINTAL(unsigned int n):
startfunction
initialize intal_result to one
if n is zero or one:
return intal_result
endif
initialize intal_num to one
create a temporary pointer temp
for i = 2 to n:
do
temp = addINTAL(intal_num,"1")
intal_num = temp
temp = multiplyINTAL(intal_num, intal_result)
free intal_result
intal_result = temp
endfor
free intal_num
return intal_result
endfunction
Bring it On!
To test your implementation of the above functions, refer to my Github repository INTAL, specifically the intal_sampletest.c file which contains a suite of test cases for the above implemented functions. You may clone the repo and have to comment out some of the function calls in the file as they are not part of this project.
You can always modify my intal_sampletest.c with any other inputs you wish to test. The only limitation is that even most modern calculators switch to exponential format after the certain number of digits, giving approximated values for really large numbers. In such cases to build the test case, you can refer to this link. This is an example for addition but the website supports all operations done in this project.
Expected Outcome
Your function should return factorial of the given input number. This milestone marks your second implemented application of INTAL. Feel free to explore the applications of INTAL in the domain of dynamic programming, such as finding Greatest Common Divisor etc.